¶ 2025_C_ST_RAIL_BUTTON_FEA
This document aims to present the method used to analyse with finite elements software the rail button of the Firehorn rocket. Indeed, this assembly is subjected to various loads during the launch.
¶ Geometry and Function
The rail button is the part directly connected to the guiding raail of Firehorn, therefore it is the part that reacts to the engine thrust. The thrustplate is also connected to the Engine bay through the thrustplate, where it is attached with 2 screws. It is made up of a chasis and a main button being attached with screws.

¶ Material
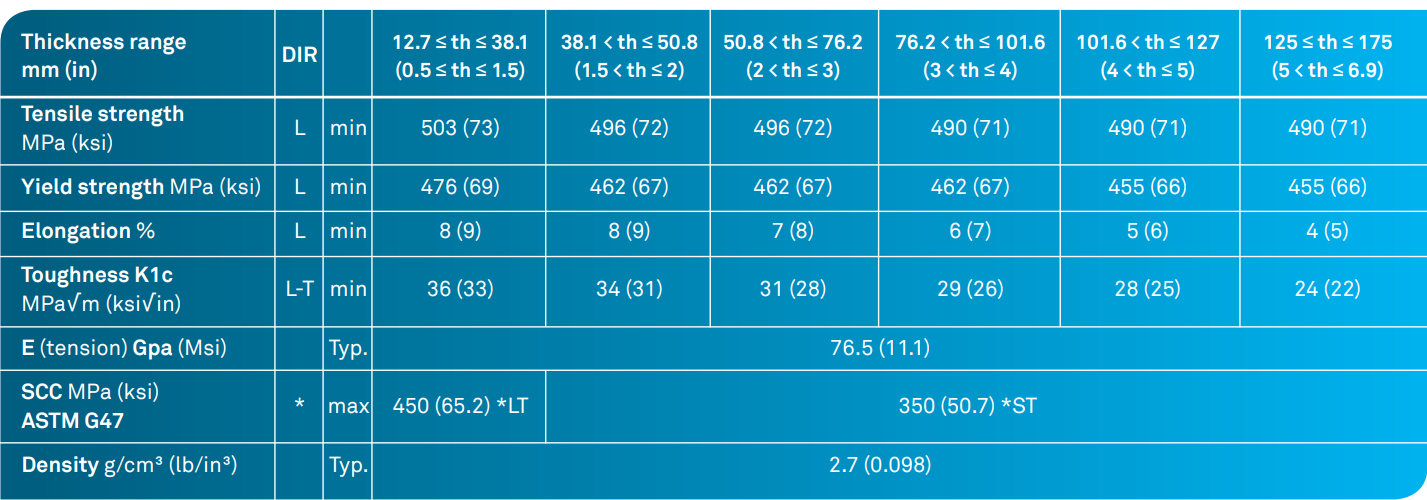
The chasis is machined in 2050-T84 alloy. This alloy has the following properties:
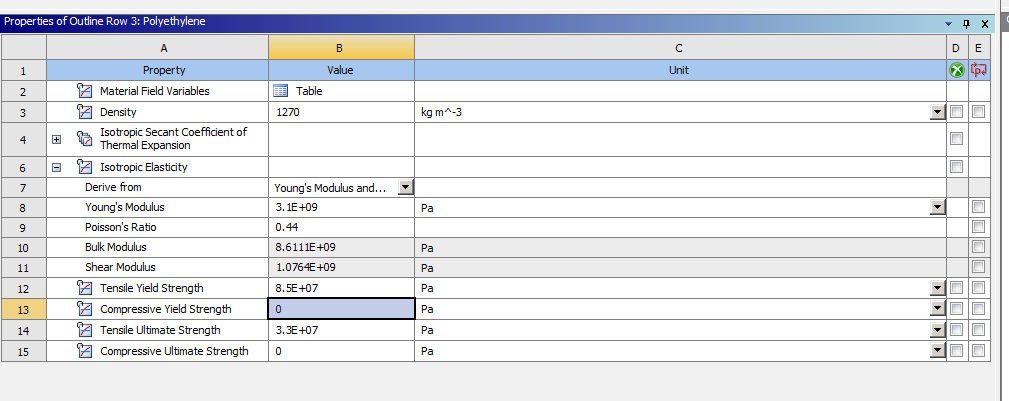
The button uses PEI which has the following properties:
¶ Load case
As said before the guides the rocket therefore the main force is applied on the inner faces of the button and can also be translated to the chasis. This force has been calculated to be 4400N.
¶ Finite Element Analysis
¶ Software
The software used for the FEA analysis was Ansys, ans the CAD of the piece was made using Solidworks
¶ Type of simulation
The simulation performed was a static structural analysis to estimate the Von mises constraints for the load case of 44400N
¶ Goal of the Simulation
The goal of the simulation is to validate that the rail button can withstand a load of 4400 kN to the designated surface with a MoS of 0.25, knowing that the material yield strength is 67 MPa for PEI and 476 MPa for the chasis.
¶ Inputs
We use the following unit system: mm-t-N-s-mV-mA
The material properties used were:
Aluminium 2050-T84

and for PEI:

The boundary counditions were:
- For the button, the screw holes were fixed supports, simulating the screws (violet) and the force is applied to the faces in contact with the rail
- For the chsis, the bottom is a fixed support as it sits on the thrustplate, and the force is applied to the screw holes, simulating the tractio force of the button

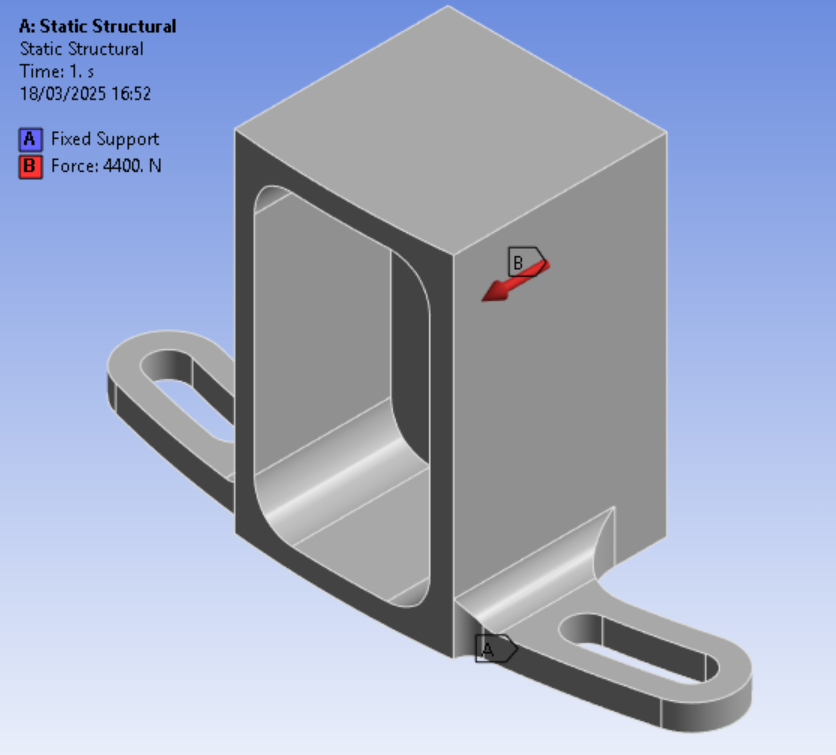
Time was not taken into account for these simulations.
¶ Mesh
¶ Different mesh used
The two meshes used were 1mm and 0.5mm
¶ Mesh refinement
No refinement has been applied.
¶ Final mesh used Example 2mm
Here is a picture of the 1mm mesh 

¶ Outputs
Here is the simulation for the 1mm mesh:
Button:
For the equivalent stress:

For the total deformation:

Chasis:
For the equivalent stress:

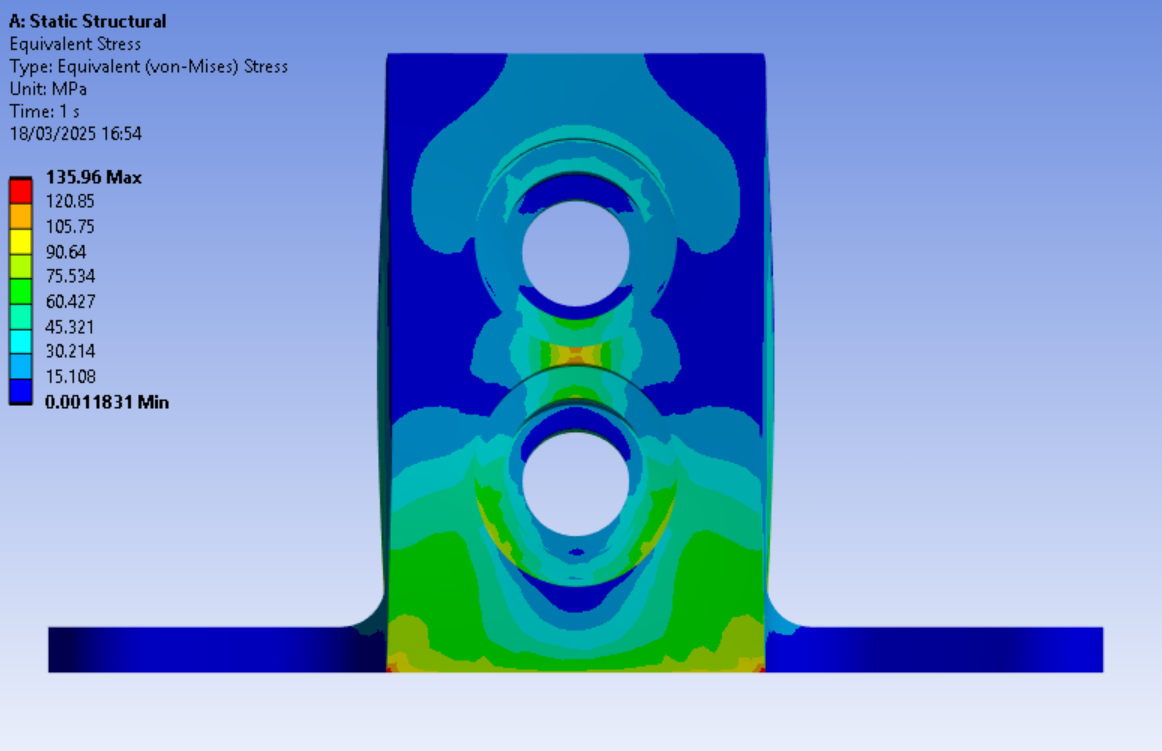
For the total deformation:
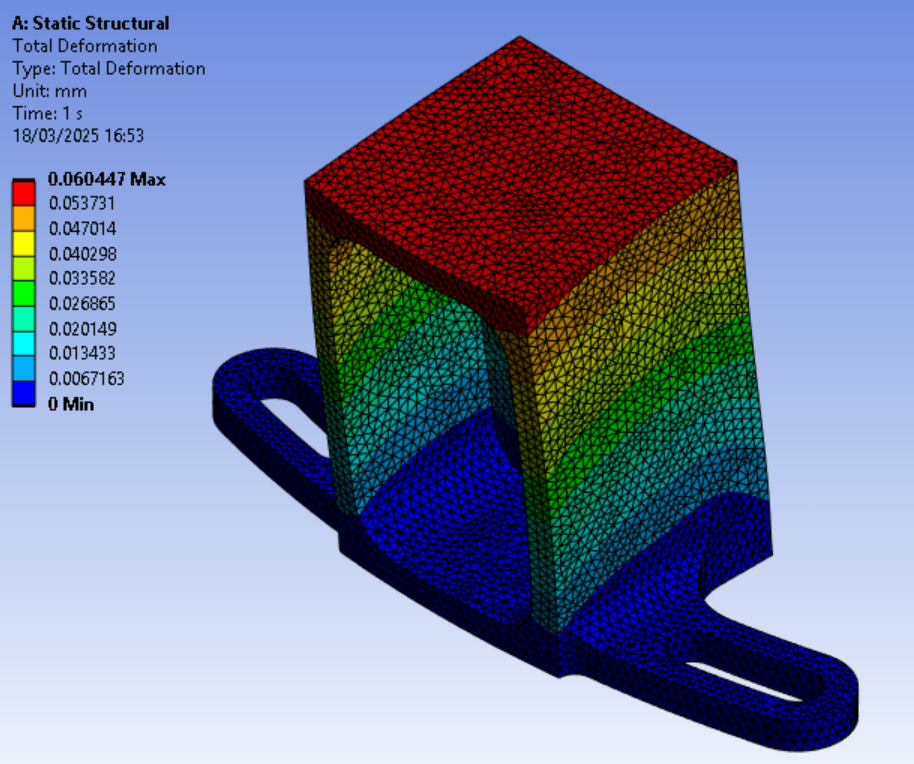
Here is the simulation for the 0.5mm mesh:
Button
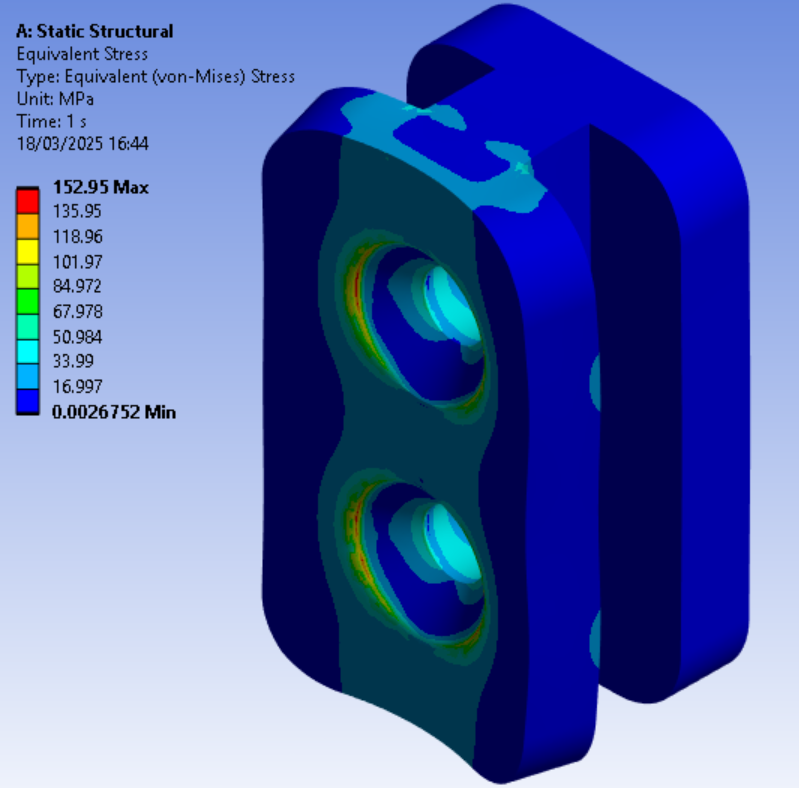
For the equivalent stress:
For the total deformation:

Chasis
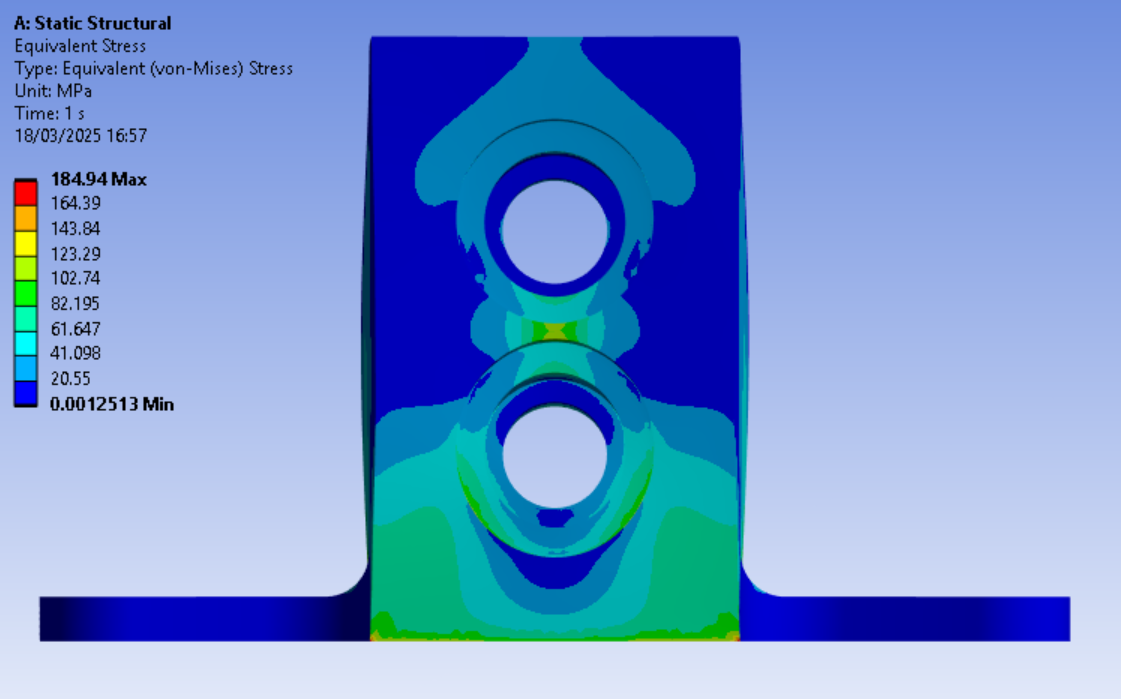
For the equivalent stress:

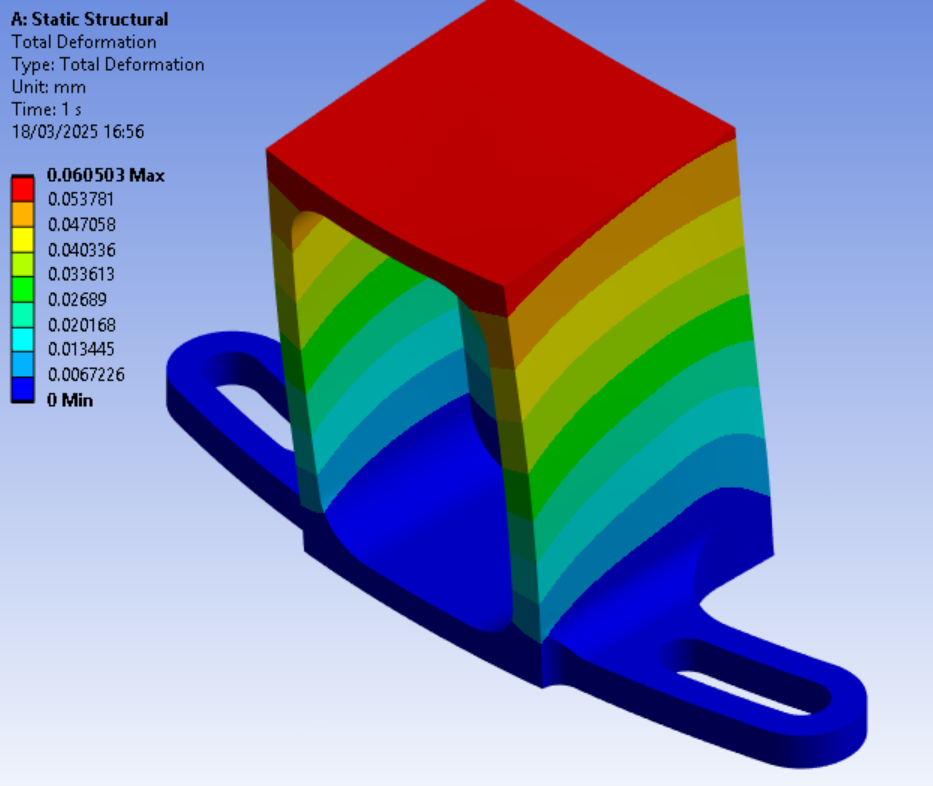
For the total deformation:
The MoS, is only attained on the chasis with a MoS of (476/185) - 1 = 1.57. The Button presents an accumulation of stress around the fixed support which we can ignore, the calculated MoS is therefore (67/51) - 1 = 0.31
¶ Conclusion
The goal of reaching a 0.25 MoS is therefore attained