¶ Hazard Analysis
¶ Written by
- Icarus Systems Engineer: Axel Juaneda
¶ Scope
This document outlines the risk analysis associated with the flights of the Icarus hopper. More informations about the CONOPS (Concept of operations) can be found here.
The goal of this analysis is to identify major risks and present their mitigation.
This risk assessment focuses exclusively on the tethered flight phase.
¶ Tank and propellant specifications
The Hopper uses N2O as oxydizer, Ethanol as fuel, and N2 to pressurize the tanks.
N2O and Ethanol are stored in a SRAD coaxial tank:
| --- | --- | --- |
| Fuel | Ethanol (90%) | 2.684 [L] |
| Oxydizer | N2O (liquid) | 7.995 [L] |
| Material | Aluminium 6082 T6 | |
| Thickness | 5mm | |
| Diameter | 140mm | |
| Length | 720mm | |
| Nominal Pressure | 40 [bars] | |
| Test Pressure | 60 [bars] | 1 [h] |
| Fail Pressure (simulated) | 80 [bars] |
The N2 is stored in a COTS COPV (volume: 2L).
¶ Risks
¶ N2O Decomposition
N2O can decompose into nitrogen (N2) and oxygen (O2) through a highly exothermic reaction, leading to possible explosions.
¶ Decomposition in the Oxidizer Tank:
Due to the large volume and pressure inside of the tank, this scenario is the most dangerous.
¶ Mitigations
- Pressurizing the system with N2 to dilute the N2O, increasing the minimal ignition energy required.
- Filling the run tank with N2O in liquid form
- Vent valve
- Pressure relief
- Burst disk
- Remotely operable filling station
- Tank and plumbing must be cleaned to avoid presence of residues (e.g. oils, greases). Those substances can trigger decomposition under high-pressure conditions.
- Filling and cleaning tank with water first to check any leaks first.
¶ Ethanol leak
Ethanol is highly flammable, so we define an ATEX zone around the vehicle.
The ATEX (Atmosphere Explosive) zone is defined based on the Lower Flammability Limit (LFL) of ethanol, where the concentration of fuel becomes sufficient to risk an explosion. For the Hopper, the maximum risk level is classified as an ATEX II zone, indicating a low explosion risk.
Our ATEX zone is defined as the area around the run tank of ethanol where an explosion can occur.
- LEL (Lower explosive limit) of ethanol in air or O2: 3.3
- Using a safety factor of 3, the safe distance from electrical equipment around the Hopper is 1.5m
The only electrical equipment present in the ATEX zone will be the Hopper's electrical systems.
Moreover, we define other mitigations :
- No heat or fire sources are allowed near the Hopper.
- Check all fittings with water and expected pressure first.
- Have a fire extinguisher close by and ready to use by anyone.
- Have the main operators do the safety fire training by the CSO.
¶ TNT Equivalent Study and Safety Distances
This section focuses on the detailed calculations necessary to estimate the TNT equivalent of the explosive potential of the Hopper. Each calculation
considers both the pressure energy and the chemical energy stored within the tanks.
The energy released during an explosion is the sum of the total pressure energy and the chemical energy of the reaction when applicable. For the reactions, we consider stoichiometric ratios, meaning the optimal fuel-to-oxidizer mix for combustion, which maximizes the amount of energy released.
¶ Computing the potential energy of pressure
The formula used to calculate the pressure energy is:
The potential energy of pressure inside a vessel is given by:
Where:
- Ph : The pressure inside the vessel (in N/m2 or Pa).
- Vh : is the volume inside the vessel (in m3).
- Pi : is the external pressure (in N/m2 or Pa).
- : is the adiabatic exponent
- U : is the potential energy of pressure inside the vessel (in Joules)
This formula applies to all pressurized tanks (Ethanol, N2O and N2 COPV)
The ETH/N2O combination operates at a pressure of 40 bars, or 4 · 106 Pa. o simplify the computations in a conservative manner, we use the following adiabatic exponents:
- for the ethanol tank, corresponding to the of N2
- for the oxidizer tank with N2O
The following pressure energy values are calculated:
- U = 17.5 kJ for ethanol
- U = 61kJ for N2O
- U = 13kJ for N2
¶ Computing the chemical energy of reaction:
There are two different reactions can result in an explosion:
- The decomposition of N2O
- The reaction between ethanol and N2O
The decomposition of N2O has an enthalpy of −82.05 kJ/mol.
For a tank of 7.995L of liquid N2O, this corresponds to 223.8 moles of N2O, releasing 18.36 MJ.
The ethanol and N2O reaction is:
The total energy released by this reaction is 187.68MJ.
¶ Conclusion
| --- | --- | --- |
| | Energy | TNT equivalent |
| ETH | 17.5 kJ | <<1kg |
| N2O | 61kJ | <<1kg |
| N2 | 13kJ | <<1kg |
| ETH + N2O | 187.76 MJ | 44.87kg |
The highest TNT equivalent calculated is 44.87kg, corresponding to the ETH and N2O reaction.
¶ Safety Distance Analysis Based on TNT Equivalent Study
This section outlines the methodology and results of calculating safety distances based on the TNT equivalent derived from previous energy calculations. The results account for the total pressure energy and chemical energy.
The Hopkinson-Cranz Scaling Law is a widely accepted method for estimating safety distances from an explosive event. It relates the distance from an explosion to the energy released, typically expressed in terms of an equivalent mass of TNT. The law is:
Where:
- R is the required safety distance (m).
- Z is a scaling coefficient, which varies depending on the scenario and acceptable risk level.
- W is the mass of the explosive material in kg, usually converted to the equivalent mass of TNT.
The value of Z depends on the context and the level of protection required. Standard values for Z based on various scenarios are:
- 8.0: Used for internal separations, such as between storage units in an ammunition storage facility.
- 14.8: For distances between explosive storehouses and public areas (e.g., roads).
- 22.2: For separation between explosive storehouses and civilian buildings, providing more protection.
- 44.4: or particularly vulnerable buildings (e.g., schools, hospitals), where the highest level of protection is needed
| --- | --- | --- | --- | --- |
| TNT equivalent | Dist. Z = 8 | Dist. Z = 14.8 | Dist. Z = 22.2 | Dist. Z = 44.4 |
| 44.87kg | 28.42m | 52.59m | 78.89m | 157.77m |
The Hopkinson-Cranz scaling law accounts only for blast overpressure effects and does not consider fragmentation hazards. Fragmentation can project high-velocity debris over significantly larger distances than predicted by blast scaling alone. A separate analysis is required to evaluate risks associated with fragmentation.
¶ Fragmentation and projectiles
¶ Hypothesis
While the blast wave determines the pressure-related safety distance, an explosion can also produce high-velocity fragments from structural breakup. These projectiles can travel farther than the blast itself and pose a serious hazard. A separate analysis is therefore performed to estimate the potential fragment speeds and associated risks.
In the following analysis, only the pressure energy is considered to evaluate the explosive effects. This is because the blast wave, driven by the rapid expansion of gases, is the main cause of damage at a distance. The chemical energy released as heat does not significantly contribute to the blast pressure and is therefore not taken into account.
The following pressure energy values were calculated:
- U = 17.5 kJ for ethanol
- U = 61kJ for N2O
- U = 13kJ for N2
We will consdier the total pressure energy as a worst case, taken as 92kJ.
¶ Initial speed
Assuming the tank explodes and the energy is transferred equally to all radial elements, the equivalent energy is:
, or .
The kinetic energy of a projectile is:
, with A the cross-sectional area and t the thickness.
Equating both, we find that:
.
For aluminimum and 5mm thick walls, we have: .
This is true for all projectiles, whatever there size.
Considering that very small projectiles do not have much energy and large projectiles do not have much perforating power, we equate the explosion of the tank to the firing of bullets in all directions.
¶ Balistic Simulation
¶ Results
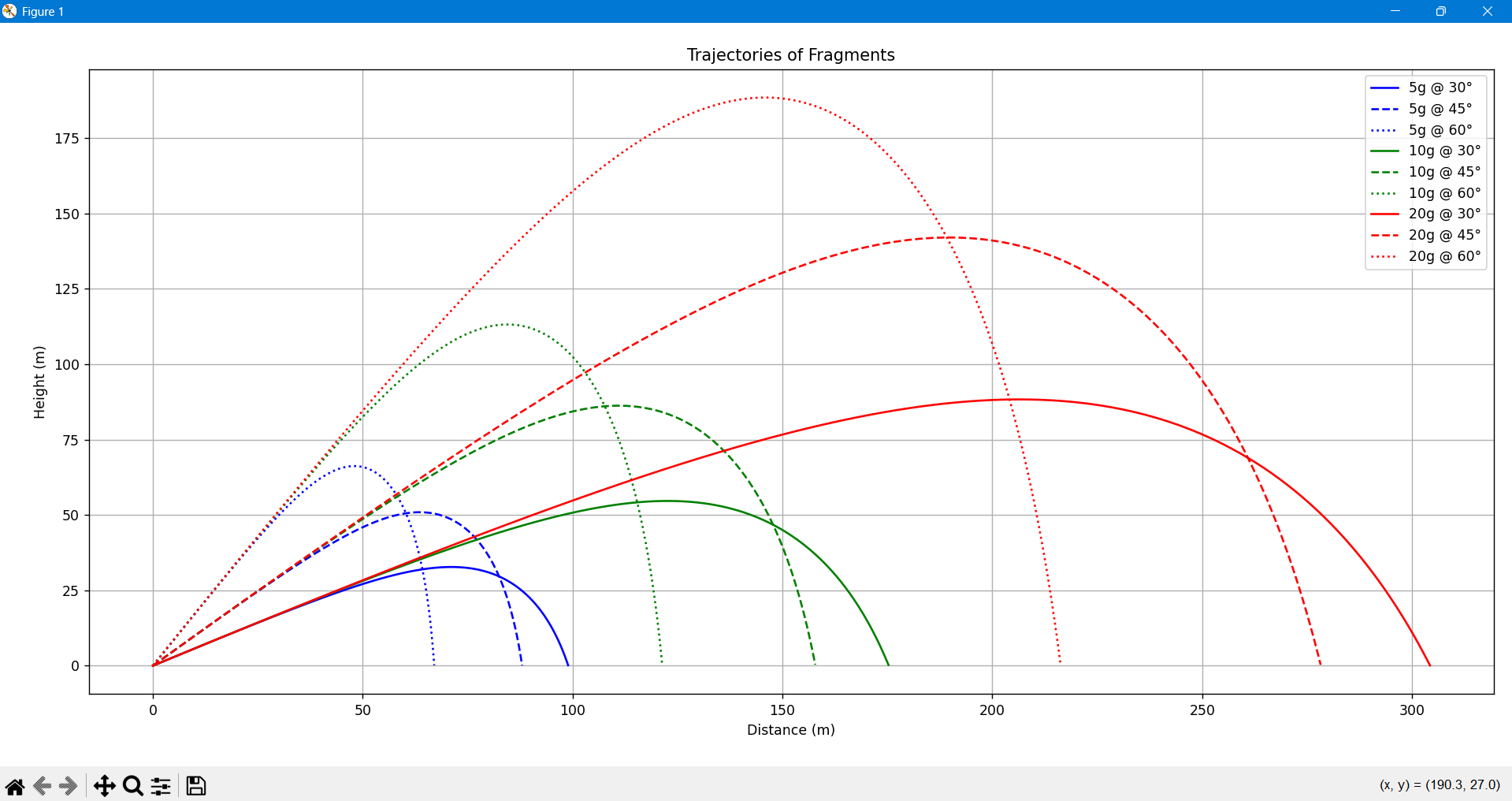
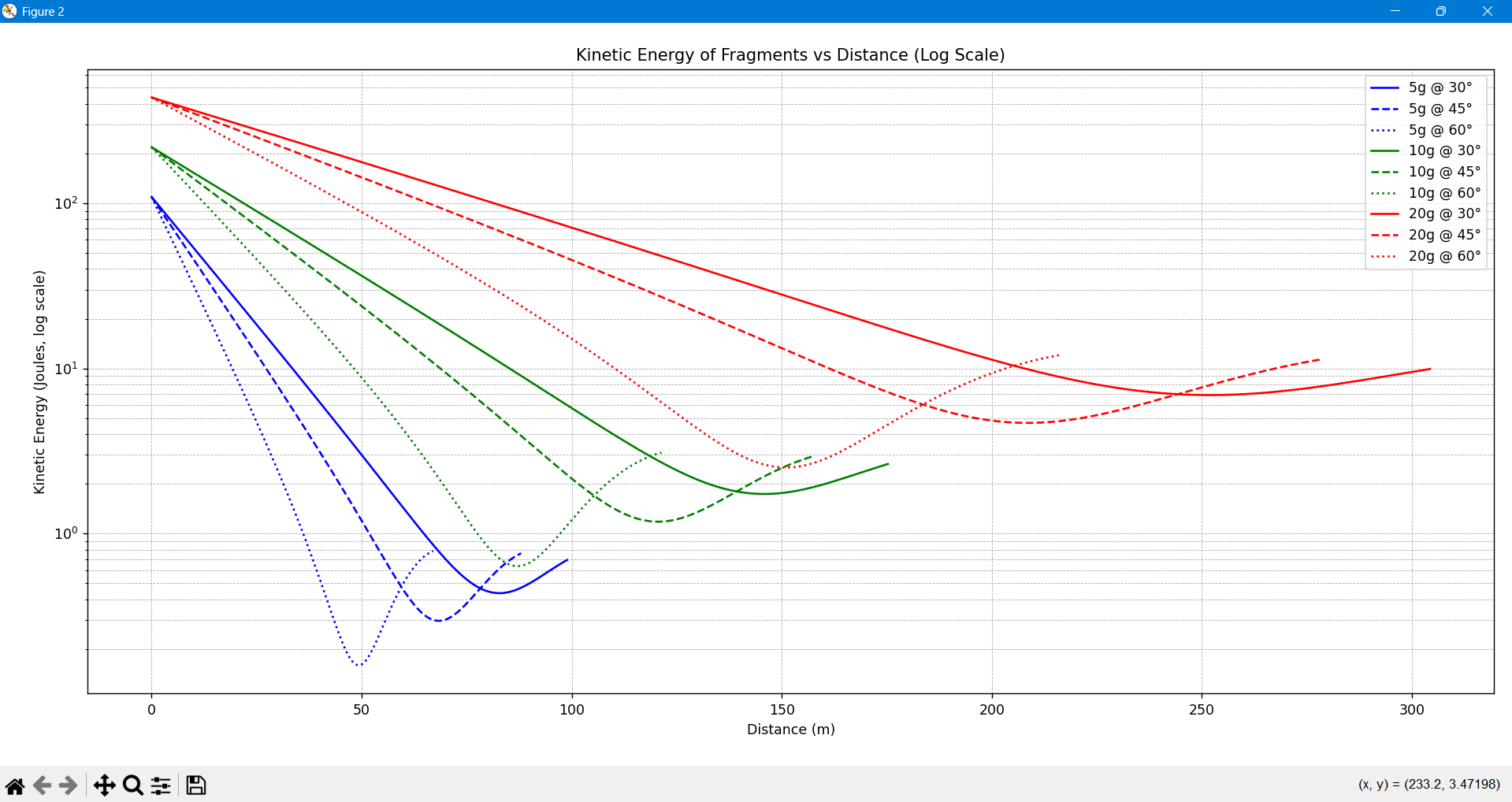
For reference, the energy of an airsoft gun typically ranges from 0.5 to 2 joules.
¶ Python Code
import numpy as np
import matplotlib.pyplot as plt
from scipy.integrate import solve_ivp
# Constants
v0 = 209.0 # Initial speed in m/s
fragment_masses = [0.005, 0.01, 0.02] # 5g, 10g, 20g
launch_angles = [30, 45, 60] # Angles in degrees
Cd = 0.5 # Drag coefficient
rho_air = 1.225 # Air density (kg/m^3)
rho_al = 2700 # Density of aluminum (kg/m^3)
g = 9.81 # Gravity (m/s^2)
# Time settings
t_span = (0, 15)
t_eval = np.linspace(*t_span, 1000)
colors = ['blue', 'green', 'red']
energy_results = {}
# Function to compute cross-sectional area for a spherical aluminum fragment
def cross_section_area(m, rho=rho_al):
r = ((3 * m) / (4 * np.pi * rho)) ** (1/3)
return np.pi * r**2
# Event: stop when projectile hits the ground
def hit_ground(t, y):
return y[1]
hit_ground.terminal = True
hit_ground.direction = -1
# --- Plot 1: Trajectories ---
plt.figure(figsize=(12, 6))
for i, m in enumerate(fragment_masses):
A = cross_section_area(m) # Dynamic area based on mass
for j, theta_deg in enumerate(launch_angles):
theta_rad = np.deg2rad(theta_deg)
vx0 = v0 * np.cos(theta_rad)
vy0 = v0 * np.sin(theta_rad)
y0 = [0, 0, vx0, vy0]
def equations(t, y):
vx, vy = y[2], y[3]
v = np.sqrt(vx**2 + vy**2)
Fd = 0.5 * rho_air * Cd * A * v
ax = -Fd * vx / m
ay = -Fd * vy / m - g
return [vx, vy, ax, ay]
sol = solve_ivp(
equations, t_span, y0,
t_eval=t_eval, events=hit_ground, rtol=1e-8
)
x, y_vals = sol.y[0], sol.y[1]
vx, vy = sol.y[2], sol.y[3]
v = np.sqrt(vx**2 + vy**2)
E_kin = 0.5 * m * v**2
label = f"{int(m * 1000)}g @ {theta_deg}°"
energy_results[label] = (x, E_kin)
plt.plot(x, y_vals, label=label, color=colors[i], linestyle=['-', '--', ':'][j])
plt.title("Trajectories of Fragments")
plt.xlabel("Distance (m)")
plt.ylabel("Height (m)")
plt.grid(True)
plt.legend()
plt.tight_layout()
# --- Plot 2: Kinetic Energy (Log Scale) ---
plt.figure(figsize=(12, 6))
for i, (label, (x, E_kin)) in enumerate(energy_results.items()):
plt.plot(x, E_kin, label=label, color=colors[i // 3], linestyle=['-', '--', ':'][i % 3])
plt.yscale("log")
plt.title("Kinetic Energy vs Distance (Log Scale)")
plt.xlabel("Distance (m)")
plt.ylabel("Kinetic Energy (Joules, log scale)")
plt.grid(True, which='both', linestyle='--', linewidth=0.5)
plt.legend()
plt.tight_layout()
plt.show()
Considering the previous assumptions, we can conclude that a security distance of more than 300 meters should be defined.
¶ Mitigations
- Add a plexiglas wall and a tent around the operators to protect them from shrapnels
- Indentify tank failure mode and protect this direction with a plexiglas wall
¶ Loss of Control
A loss of control of the vehicle could occur due to various factors, such as a mistuned controller, electrical failure, or propulsion malfunction.
¶ Mitigations
To ensure maximum safety in this situation, several mitigation measures have been implemented:
- The Hopper will be securely attached and supported by a crane.
- The Hopper is equipped with an independent flight termination system that can be activated at any time by the operators.
- The Hopper’s flight computer is capable of automatically triggering an abort procedure in the event of non-nominal states or upon operator command.